グレーティング

講座1
「分光」。それは「光」を「分ける」ことですが、その技術には歴史があります。 ニュートンがプリズムで初めて分光を発見した時代から最先端の分光技術まで、この歴史を知ることにより、光の謎を解き明かす旅へ出かけませんか?
グレーティング(回折格子)の製造には、古くからあるルーリングエンジンを用いる製法と、2本のレーザー光の交差で生じる干渉縞を利用したホログラフィック製法によるものがある。
回折格子は、ダイヤモンド・カッターで溝を削っていく、古くからあるルールドエンジンを用いるクラシカルな製法と、2本のレーザー光の交差で生じる干渉縞を利用するホログラフィック製法で製造されています。
古くからある製法のルールドグレーティングは、形状は平面でその表面に溝が隣り同士平行に刻まれています。ホログラフィックグレーティングの溝は、隣同士平行の場合もあれば、分光光学系の性能を最適化するために、曲率をもった不等間隔になっている場合もあります。またホログラフィックグレーティングは、平面、球面、トロイダル面、その他多くの形状の表面に溝をつくることができます。
グレーティング(回折格子)とは、2本のレーザー光の交差により生じる干渉縞を利用して製造されるホログラフィクタイプと、古くからある ルーリングエンジンを利用して製造される、ルーリングタイプのものがある。
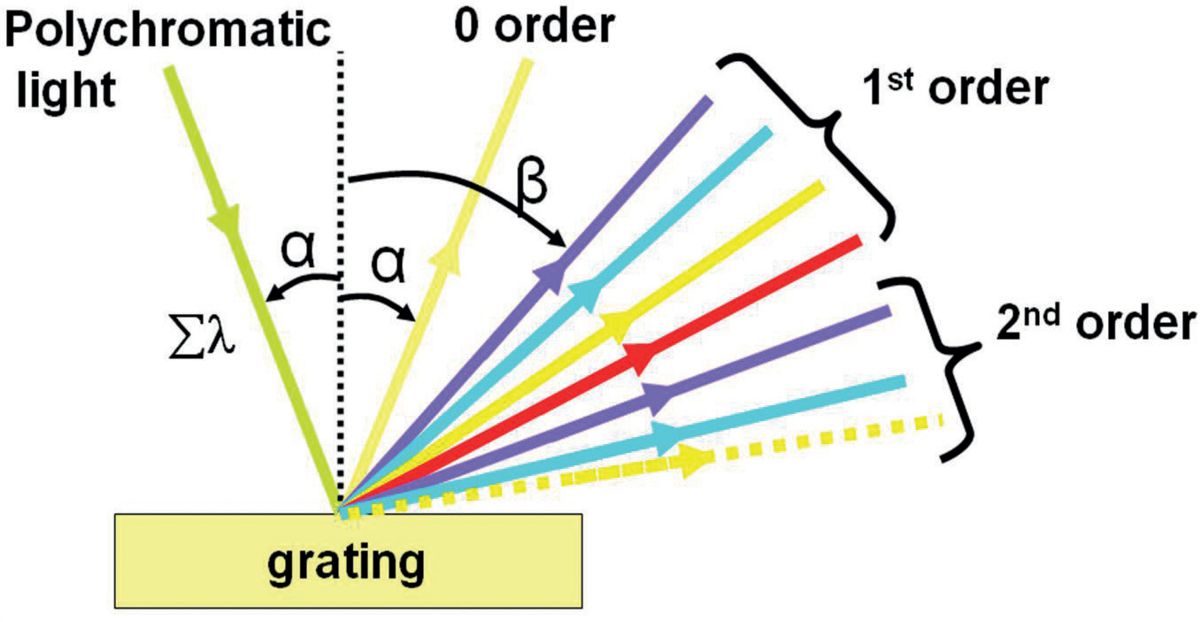
グレーティング方程式:定義と単位
基本式を紹介する前に、まず単色光と連続スペクトルについて簡単に説明します。
単色光はスペクトルの幅が限りなく狭い光です。このような光に非常に近い光源として、シングルモードレーザーや超低圧冷却型の分光校正ランプがあります。これらは、「ライン」または「ディスクリートライン」光源とも呼ばれます。
連続スペクトルは、例えば「白色光」のように、有限のスペクトル幅を持っています。原理的にすべての波長が存在しますが、実際には "連続スペクトル "はほとんどの場合、あるスペクトルのセグメント(ある領域の幅)をなしています。連続スペクトルのセグメントの幅がナノメートルの数分の1しかなく、線スペクトルに似ていることもあります。
以下の方程式は、μ0 = 1 の空気中のシステムに対するものです。したがって、空気中では、λ = λ0 となります。
\({\lambda}_0={\lambda}/μ_0 \)
\(1nm=10^{-6}mm \)
\(1Å=10^{-7}mm \)
最も基本的な回折格子方程式: (1) \(\sin{\alpha}+\sin{\beta}=10^{-6}kn{\lambda} \)
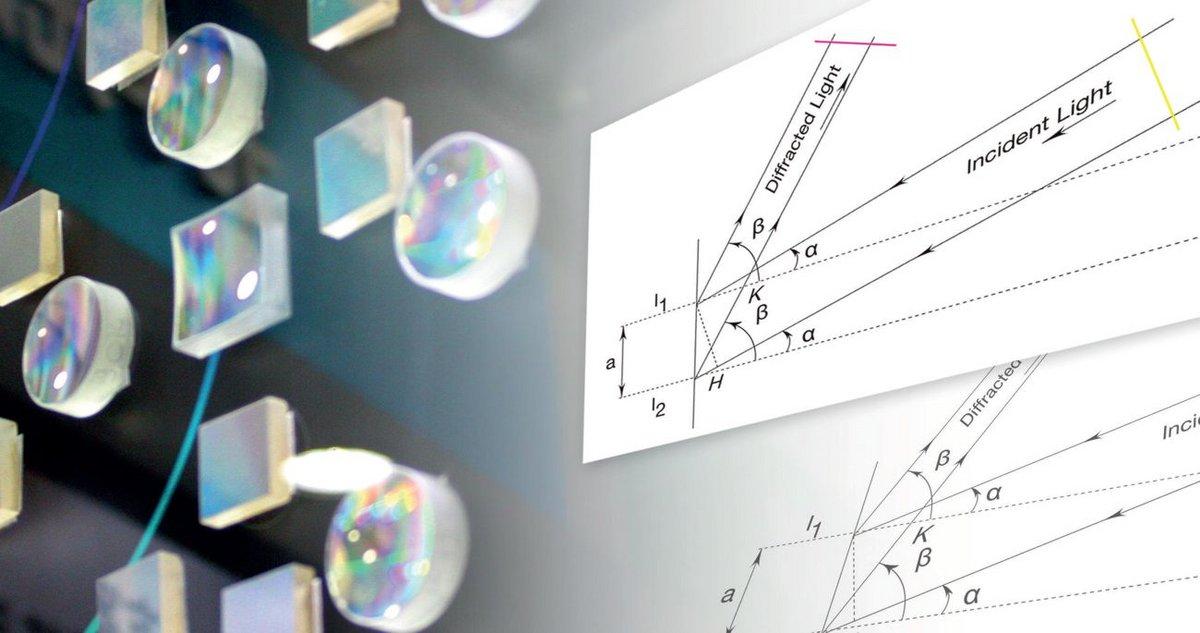
図1.多くのモノクロメータでは、入口と出口のスリットの位置は固定されており、グレーティングはその面の中心を通る平面の周りを回転する。そのため、角度Dvは一定である。
ほとんどのモノクロメーターでは、入口と出口のスリットの位置は固定されており、グレーティングはその面の中心を通る平面の周りを回転します。したがって、角度DVは、以下の式で決定される定数です。
(2) \(D_V={\beta}-{\alpha} \)
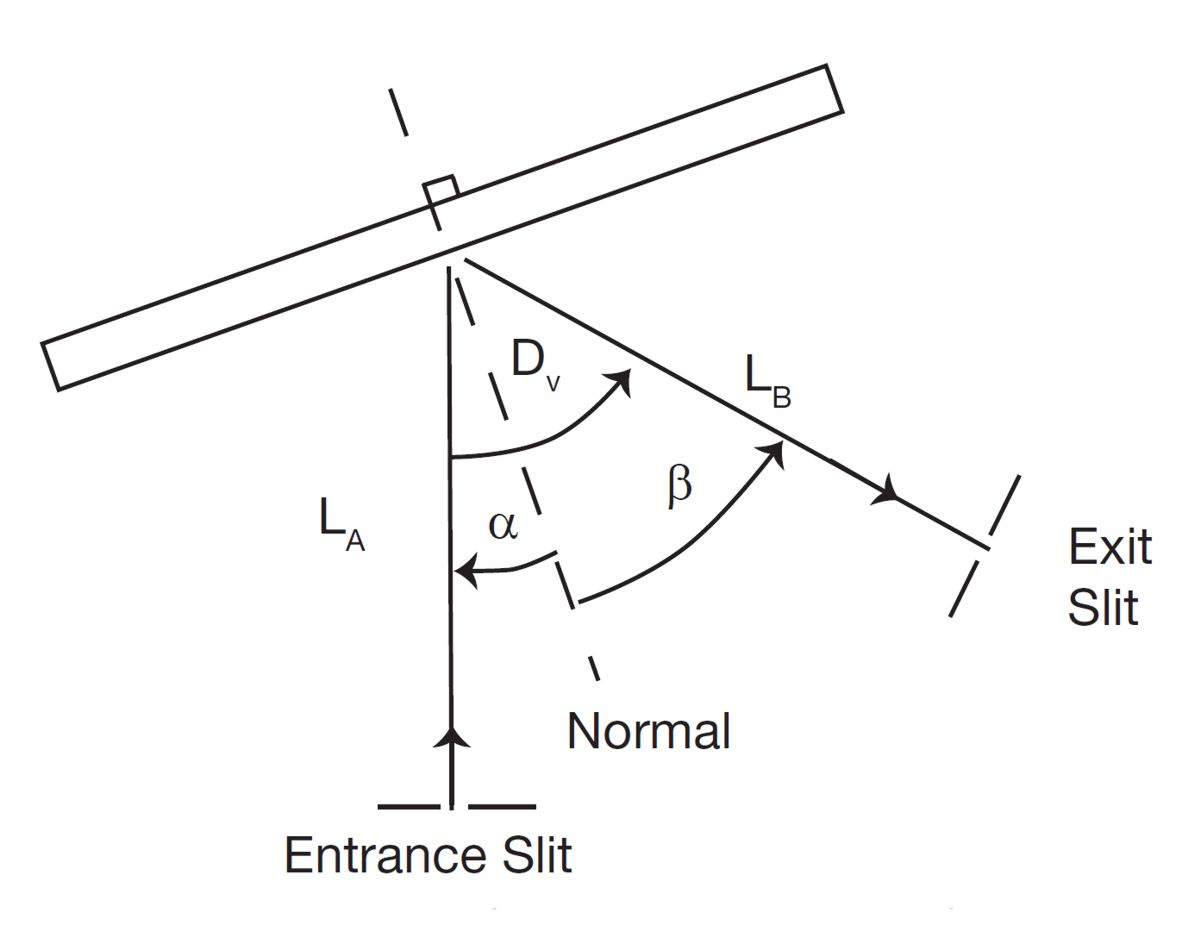
図2.モノクロメーターの構成図
ある波長(1)に対してαとβの値を決めたい場合、回折格子式は次のように表すことができます。
(3) \(10^{-6}kn{\lambda}=2\sin[\frac{(\beta+\alpha)}{2}]\cos[\frac{(\beta-\alpha)}{2}] \)
DVの値がわかっている場合、αとβは式(2)と式(3)により求めることができます(図2、図3参照)。
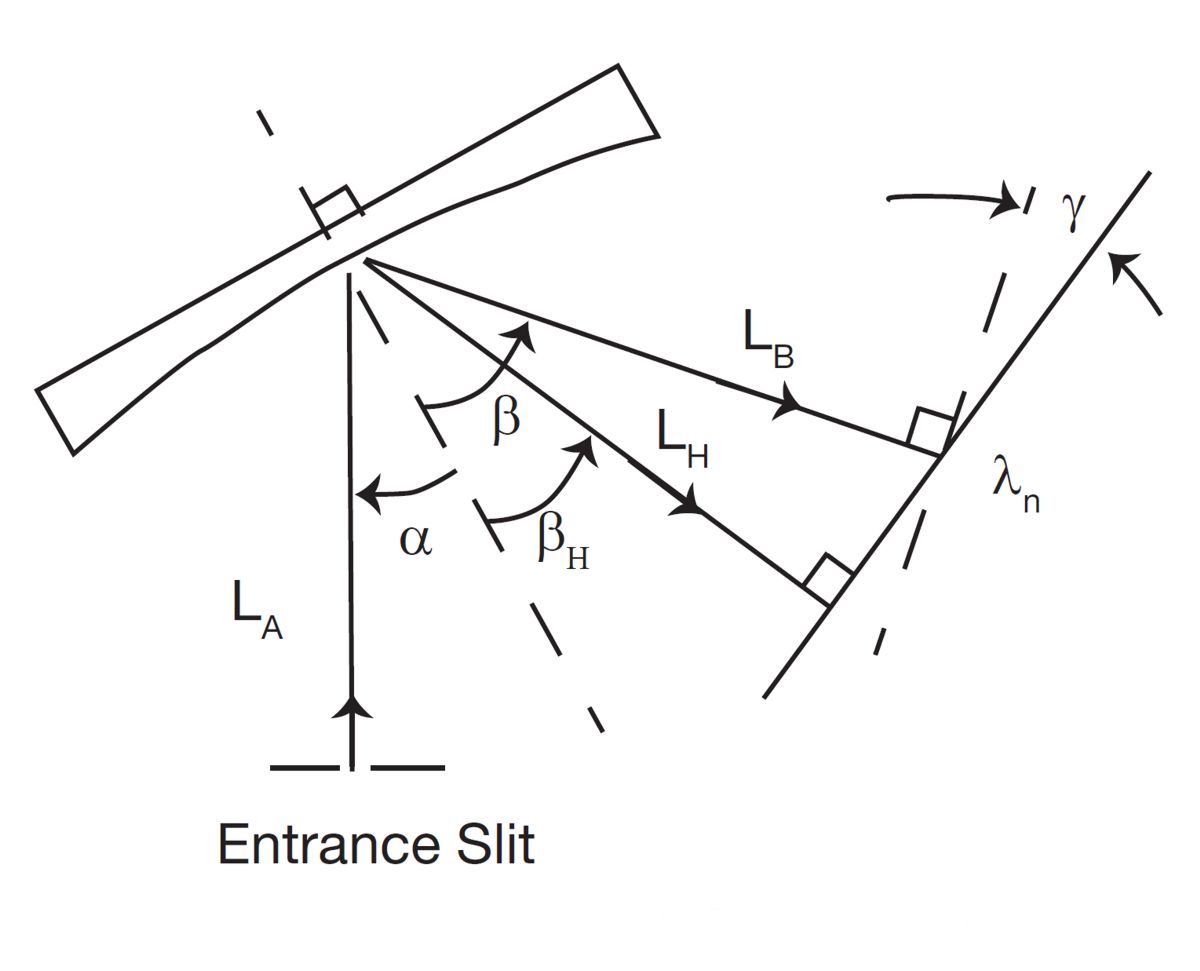
図3.スペクトログラフの構成図
LA = 入射アーム長
LB = λnでの出射アーム長
βH = スペクトル平面への垂線とグレーティング法線との間の角度
LH = スペクトル平面からグレーティングまでの垂直距離
表1は1200 gr/mmのグレーティングで、500nmの回折光を得るように設定した際、入射角と回折角が 偏角Dvでどの様に変化するかを示す。
表1は、図2に基づいて、モノクロメーターの光学配置で、1200 gr/mmのグレーティングを用い、500nmの回折光を得られる様に設定した際、入射角αと回折角βが偏角DVによってどのように変化するかを示したものになります。
(4)\(\frac{d{\beta}}{d{\lambda}}=\frac{kn10^{-6}}{\cos{\beta}} \) rad/nm
dβ = 2つの波長間の角度分離 (ラジアン)
dλ = 2つの波長間の微分距離 (nm)
線形分散とは、分光器の焦点面に対して(すなわちスリットの位置で)、どの程度スペクトルが広がっているかを示すもので、nm/mm、Å/mm、cm-1/mm などで表現されます。例えば、2つの分光器を考えてみます。1つは、0.1 nmのスペクトル間隔を1 mmの幅に広げる(すなわち分散させる)分光器と、もうひとつは10 nmのスペクトル間隔を1 mmの幅に広げる(分散させる)分光器があるとします。
1台目の分光器の方が2台目のよりも、より細かくスペクトルを確認する事ができるだろうということは容易に想像できます。
これは、1台目の分光器の方が、2台目の分光器に対して「高い」分散をもつこと – すなわち2台目の分光器の方が「低い」分散をもつことを示しています。線形分散は、分光器のスペクトルを細かく分離する能力と関連しています。
中心波長λで回折光に垂直な線形分散は、次式で求められます。
(5) \(\frac{d{\lambda}}{dx}=\frac{10^6{\cos}{\beta}}{knL_B} \) nm/mm
ここで、LBは有効射出焦点距離(mm)、dxは焦点面に沿った単位間隔(mm)です(図2参照)。
モノクロメータでは、LBは集光ミラーから出射スリットまでのアーム長、グレーティングが凹型の場合はグレーティングから出射スリットまでのアーム長です。したがって、線形分散はcosβに直接比例し、出射アーム長(LB)、回折次数(k)、溝密度 (n) に反比例して変化します。
スペクトログラフでは、スペクトル平面に垂直な波長λn以外の波長に対する線形分散は、波長λnにおける傾斜角(γ)の余弦(cosγ)によって変化します。図3は、リニアダイオードアレイを使用した「フラットフィールド」スペクトログラフです。
(6) \(\frac{d{\lambda}_0}{dx}=\frac{10^6{\cos}{\beta}{\cos}{\gamma}}{knL_{B{\lambda}n}} \)
(7) \(\gamma={\beta}_H-{\beta} \)
(8) \(\frac{d{\lambda}_0}{dx}=\frac{10^6{\cos}{\beta}{\cos}^2{\gamma}}{knL_H} \)
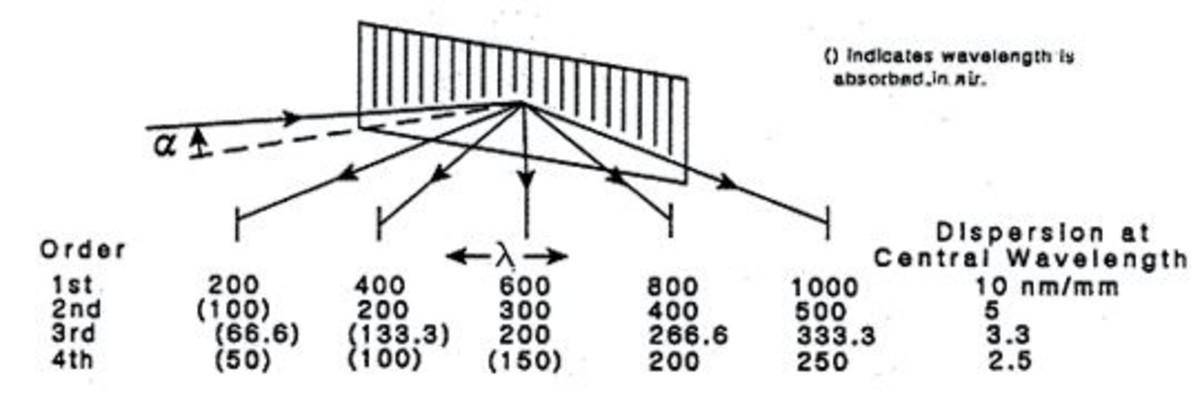
図4.200〜1000nmの1次スペクトルが焦点面に広がる分光器構成
図4は、スペクトログラフの光学配置で、焦点面上に広がった200~1000 nmの1次スペクトルを示します。方程式(1)から、グレーティングの溝本数と、αとβが与えられると:
(9) \(k{\lambda}=\text{constant} \)
と表せます。その結果、もし回折次数kが2倍になるとλが半分になる、等々の結果が得られます。
例えば、光源が200nmから1000nmまでの連続した波長を発している場合、物理的に1次の800nmの位置(図4)には、400、266.6、200nmの波長も存在し、同じ検出器で観測されます。800nmの光だけを観測するためには、フィルターを用いて高次の波長を除去する必要があります。
190nm以下の波長は空気に吸収されるため、200~380nmの1次波長はフィルターなしでモニターすることができます。しかし、装置内を真空にしたり、N2パージすると、(190nm以下の波長を吸収する空気が無くなるため)、再び高次のフィルターが必要になります。
Resolving “ Power” 「分解能」(理論値)は、次式で与えられます。
(10) \(R=\frac{\lambda}{d{\lambda}} \) (dimensionless)
ここで、dλは強度が等しい2つのスペクトル線の波長差です。分解能とは、隣接するスペクトル線を分離する装置の能力をいいます。もし2つのピーク間の距離が、一方のピークの最大値が他方のピークの最初の最小値の位置にあった場合、これら2つの波長は分離されているとみなされます。これはレイリー基準と呼ばれます。
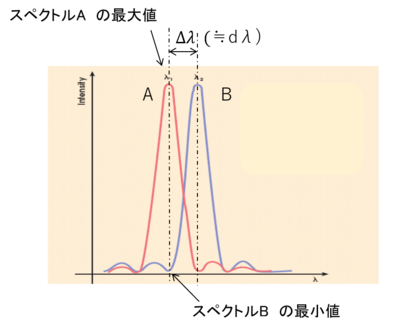
スペクトルBの最小値にスペクトルAの最大値があると、2つのスペクトルは分離して見える。
分解能は、以下のように示すことができます。
(11) \(R=\frac{\lambda}{d{\lambda}}=knW_g=kN \)
λ = 分離されるスペクトル線の中心波長
Wg = グレーティングに照射される入射光の幅
N = グレーティングの溝の総数
この数値で表される分解能、数値分解能 "R "は、装置の分解能やバンドパスと混同しないようにする必要があります。
理論的には1次で使用される、幅110mmの1200g/mmグレーティングの、数値分解能はR = 1200 × 110 = 132,000となります。したがって、500nmでは、バンドパスは、次のようになります。
dλ= 500/132,000 = 0.0038 nm
しかしながら、実際の装置では、(1)式によって幾何学配置が決定されます。
kについて解くと
(12) \(k=\frac{\sin{\alpha}+\sin{\beta}}{10^{-6}n{\lambda}} \)
しかし、回折格子の刻線幅Wgは
(13) \(W_g=\frac{N}{n} \) then \(N=W_gn \)
ここで \(\frac{1}{n} \) mm/gr
(12)と(13)を(11)に代入すると、分解能は次のように表すこともできます。
(14) \(R=W_g\frac{\sin{\alpha}+\sin{\beta}}{10^{-6}{\lambda}} \)
従って、回折格子の分解能は以下の条件に依存することになります。
バンドパスは分光器のスリット幅と残留収差によっても決まるため、このレベルで達成されるバンドパスは100%理論通りにいかないため、装置の回折限界内でのみ可能となります。
ブレーズとは、あるスペクトルの領域をゼロ次以外の任意の次数に集中させる事として定義されています。ブレーズグレーティングは、指定された波長で最大の効率が得られる様に作られています。したがって、グレーティングの溝形状を適切に選択することにより、「250nmでブレーズ」、「1ミクロンでブレーズ」などと表現することができます。
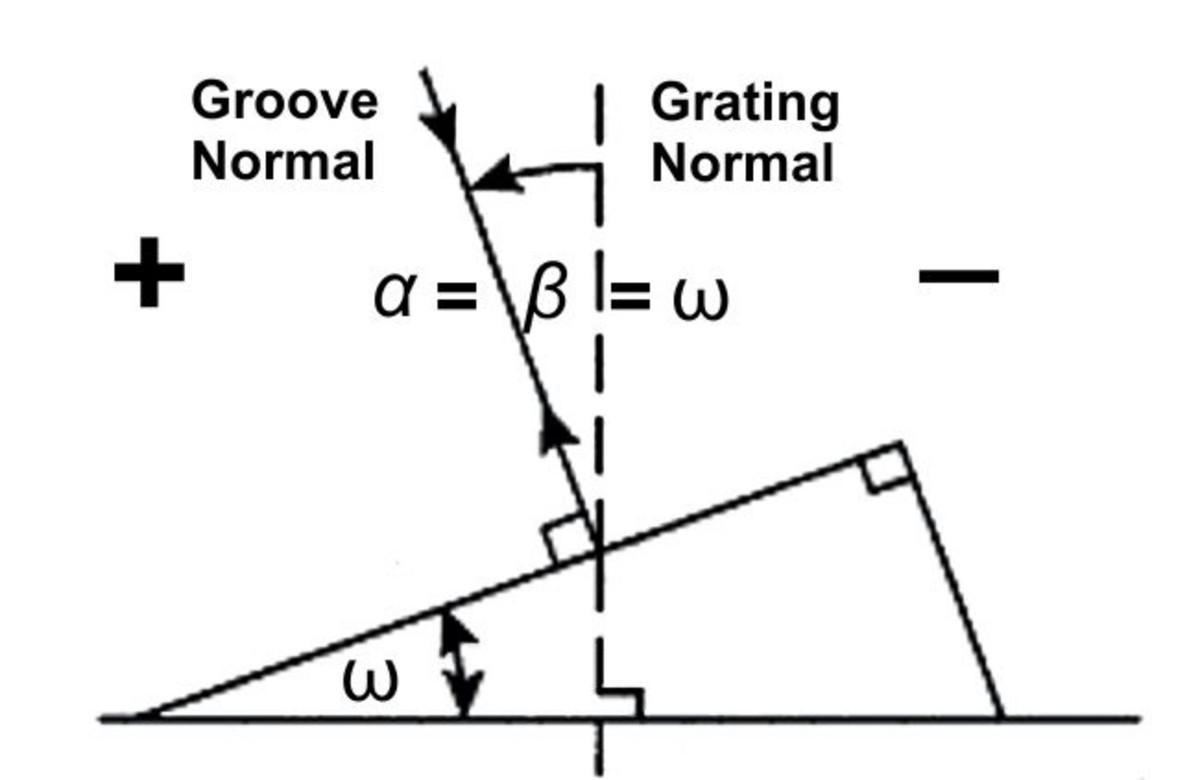
ブレーズグレーティングとは、図5に示すように、グレーティングの溝が「ブレーズ角ω」を持つ直角三角形をなすように制御されたグレーティングのことです。ただし、特にブレーズホログラフィックグレーティングでは頂角が110°まで存在することがあります。三角形の溝の頂角を上手く選択する事で、グレーティングの全体的な効率形状を最適化することができます。
図5.ブレーズグレーティングの溝形状はリトロー条件で計算されている。ここでリトロー条件とは、入射光と回折光がオートコリメーション(α=β:入射角と回折角が等しい)の関係にある状態をいう。
ブレーズド・グレーティング溝形状は、入射光と回折光がオートコリメーション(すなわち、α = β)となるリトロー条件で計算されています。したがって、入射光と回折光は、同じ軸に沿って伝搬していきます。
この場合、「ブレーズ」波長λBでは、
\(\sin{\alpha}+\sin{\beta}=kn{\lambda}_B10^{-6} \) から、
(15)\(\omega=\alpha=\beta \) ここで\(\omega= \)ブレーズ角
\(2\sin{\omega}=kn{\lambda}_B10^{-6} \)
例えば、250nmでブレーズ化した1200g/mmグレーティングのブレーズ角(ω)は、1次(k=1)で8.63°になります。
特に断りのない限り、グレーティングの効率は、与えられた波長において、リトロー配置で測定されたものになります。
(16) \(\text{%絶対効率}=\frac{\text{energy out}}{\text{energy in}}\times\frac{100}{1} \)
(17) \(\text{%相対効率}=\frac{\text{grating efficiency}}{\text{mirror efficiency}}\times\frac{100}{1} \)
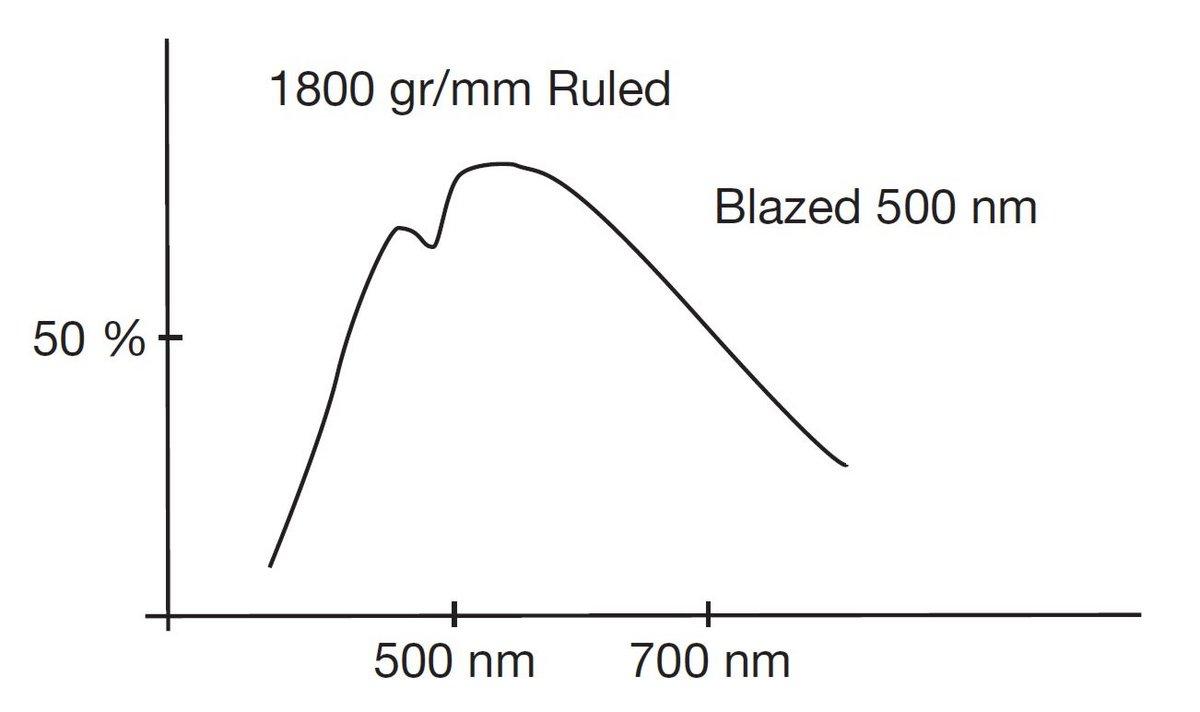
図6.ブレーズド・ルールド・グレーティングの典型的な効率曲線
相対効率の測定には、グレーティングと同じ材質でコーティングされたミラーの効率をグレーティングと同じ角度で測定することが必要です。
ブレーズグレーティングとホログラフィックグレーティングの典型的な効率曲線は、それぞれ図6と図7を参照してください。
一般的な近似値として、ブレーズグレーティングでは、ブレーズ波長の2/3、1.8倍の波長で効率が50%減少します。
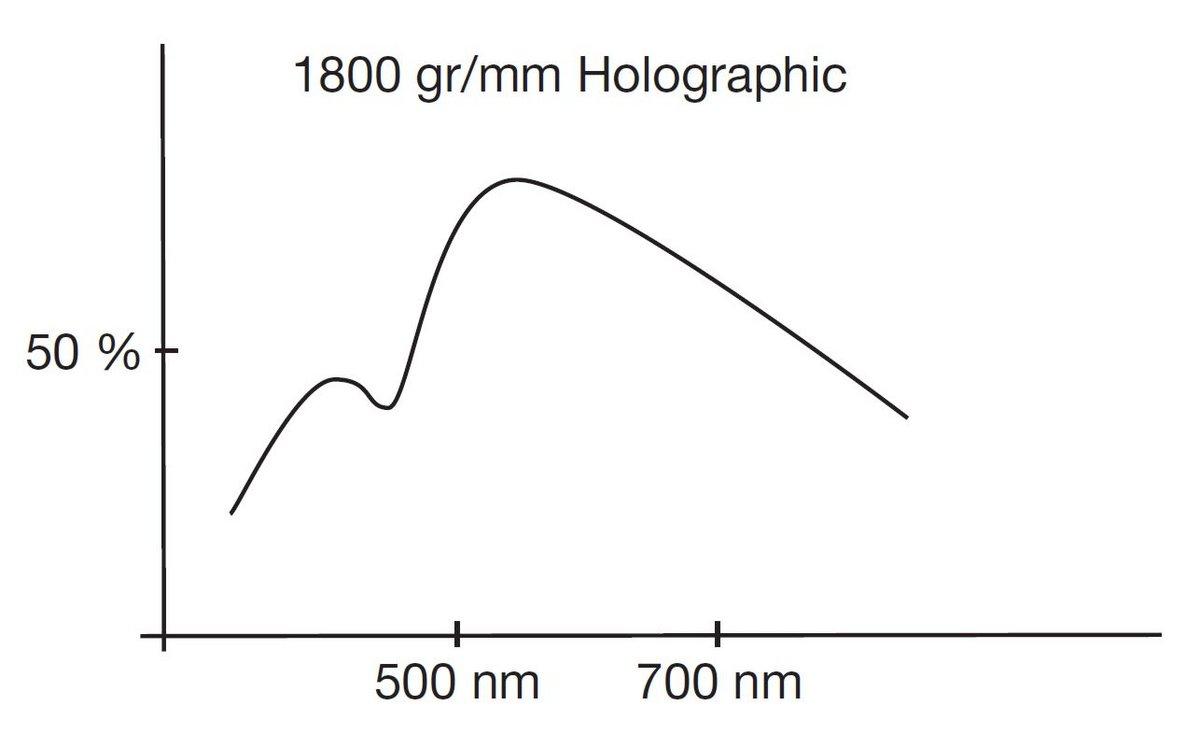
図7.非ブレーズ型ホログラフィックグレーティングで高効率をもつ例
1次でブレーズされたグレーティングは、それ以上の次数でも同様にブレーズされたものになります。したがって、1次で600 nmにブレーズされたグレーティングは、また2次では300 nmにブレーズされたものになり、以下同様です。
高次の効率は、通常、1次の効率曲線に従います。1次でブレーズされたグレーティングでは、次数kが大きくなるにつれて、後続の高次それぞれの最大効率が減少していきます。
効率はまた、グレーティングが使用されるリトロー条件から離れるほど(例えば、α≠β)、減少していきます。
ホログラフィックグレーティングは、高次光を抑えるような溝形状を有するように設計することができます。これは、イオンエッチングで作成されたラミナー形状(準矩形)を使用するUVおよびVISで特に効果的です。
注:グレーティングが「ノン・ブレーズ(ブレーズ無し)」だからといって、必ずしも効率が悪いとは限りません。図7は、1800 g/mm の正弦波状の溝形状を持つホログラフィックグレーティングの効率曲線を示しています。
検出器に到達する目的の波長以外の光(多くの場合、1つまたは複数の「散乱光」の要素を含む)は迷光と呼ばれます。
散乱光は、以下のいずれかによって発生する可能性があります。
ルールドグレーティングとホログラフィクグレーティングの迷光の違い
もしグレーティングに周期的な刻線誤差があると、ゴースト (それは散乱光ではありません) が分散平面上に像を結びます。ゴーストの強度は次式で与えられます。
(18) \(I_G=I_Pn^2k^2e^2π^2 \)
where,
IG = ゴースト強度
IP = ペアレント強度
n = 溝の密度
k = 次数
e = 溝の位置の誤差
ゴーストはモノクロメーターの分散平面状に集光し、像を結びます。ホログラフィックグレーティングの迷光は、通常、ルールドグレーティングの10分の1程度で、集光はせず、それがある場合は、2πステラジアンで放射されます。
ホログラフィックグレーティングは、周期的な刻線誤差がないためゴーストが発生せず、ゴースト問題に対する最良の解決策となります。
ここで、ゴーストとそれに続く迷光の強さは、次数と溝密度の2乗に比例することを思い起こしておきましょう。
(式(17)よりn2、k2)。ルールドグレーティングを高次または高溝密度で使用する場合は注意が必要です。
HORIBAは、「Your Partner in Science」をテーマにオンラインセミナーで、各種分析の基礎やノウハウを紹介しています。皆様からのご視聴お申込みを心よりお待ち申し上げております。
粒子計測、蛍光X線分析、元素分析、分光分析、ラマン分光分析、蛍光分光分析、表面分析の基礎やノウハウを紹介したセミナー(アーカイブ動画)の一覧です。