The Concept of Conductivity
Theory and practical measurement of conductivity

Just as electrons play an important role when an electric current passes through a solid material such as an electric wire, ions (cations that carry a positive (+) charge and anions that carry a negative (-) charge) have an essential role when a current passes through a liquid, such as an aqueous solution.
Since conductivity is an indicator of how easily current passes through a solution, it is dependent on the quantity of ions and their mobility in that solution.
Ohm’s famous law provides the fundamental rule here. Ohm’s law states that the current (I) passing through an electric wire or similar conductor is proportional to the voltage (E) across it, and inversely proportional to its resistance (R). In other words,
I=E/R
where I is the current (ampere: A), E is the voltage (volt: V), and R is the resistance (ohm: Ω).
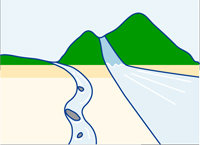
If we liken the principle behind Ohm’s law to the situation in a river, the volume of water that flows corresponds to the current, the height difference along the river corresponds to the voltage, and the length and width of the river and the obstacles within it correspond to the resistance.
This means that the greater the difference in height (voltage), and the fewer obstacles in the river (resistance), the greater the volume of water that will flow (current).
This can also be applied to the current passing through a solution. Let us consider the inverse of resistance (R). Since resistance resists current, its reciprocal provides an indicator of how easily current flows. Let this indicator be K, so that 1/R = K. Hence, the current passing through a solution is given by
I = K • E
where I is the current (ampere: A), E is the voltage (volt: V), and K is the conductance (siemens: S). * Siemens S is the reciprocal of resistance (Ω).
Note that a difference exists between the situation in solutions and that in the solid state. For an aqueous solution, applying a constant voltage (DC voltage) across two electrodes causes electrolysis of the water. To prevent this, an alternating voltage (AC voltage) is applied when measuring conductivity, commercial power sources of 50 Hz or 60 Hz usually being used. Conductivity meters, which use a battery as their power source, provide an AC voltage to their sensor electrodes by converting DC to AC.
Let us consider resistance R (Ω) once again. As might be expected from the river analogy, resistance R is proportional to the length of the conductor—such as an electric wire—and inversely proportional to its cross-sectional area. Hence
R = r • L / S, where r is the resistivity, L is the length (cm), and S is the cross-sectional area (cm2).
This shows that r (resistivity) is in units of Ω/cm. Let us also designate L/S as the cell constant a, with units of cm-1.
The reciprocal of r, 1 / r = k, is known as the specific conductivity. In general, k is referred to simply as conductivity. Hence, k = 1 / r = a / R, and is in units of S/cm.
One thousandth of the unit of resistivity S/cm is mS/cm, and one thousandth of that is μS/cm.
The SI unit system uses μS/cm, mS/m, and S/m; 1 μS/cm = 100 μS/m = 0.1 mS/m.
Generally available conductivity measurement cells (electrodes) have cell constants a = 0.1 cm-1, 1 cm-1, or 10 cm-1. In SI units, these are a = 10 m-1, 100 m-1, and 1,000 m-1, respectively.
![]()
Electricity and Ohm's Law
Do you remember Ohm's law, which you learned about in junior high school? Of course, not many people need to use Ohm’s law in their everyday lives, so here we will explain its essential concept.
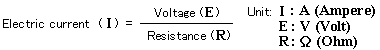
It may seem premature to suddenly produce an equation like this, but the above formula describes Ohm’s famous law.
In our houses in Japan, we use electricity of 100 volts, and D and C-batteries produce 1.5 volts. These values are voltages.
When you connect a small bulb to a battery, the bulb glows, because an electric current passes through it. The current is hindered by what we call resistance, and the larger the resistance, the harder it is for the current to flow.
Compare the principle behind Ohm’s law to the situation in a river. The height difference along the river correspondents to the voltage and the volume of water that flows corresponds to the current. The length and width of the river, and the obstacles within it, correspond to the resistance.
This means that the greater the difference in height, and the wider and shorter the river and the fewer the obstacles, the greater the volume of water that will flow.
To help refresh your memory, please answer the following question:
Question: How much current (in amperes) flows when a small bulb with a resistance (when lit) of 3 ohms is connected to a 1.5-V D-battery?
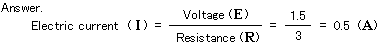
Next page Ions in Water, and Conductivity