What Is ORP?

Most electrochemistry- or electrochemical analysis-related handbooks or books consistently contain the following table as examples of oxidation-reduction potentials:

Table 1 Oxidation-Reduction Potentials

“Analytical Chemistry Data Book”* (1970), The Japan Society for Analytical Chemistry, p. 89, Maruzen (* This book is only available in Japanese. The title is a provisional translation.)

In this table, as the value of E⁰ (oxidation-reduction potential) is increased, the tendency to reduction also increases, and as the value is decreased, the tendency to oxidization increases. Some examples in this table can be read as follows:

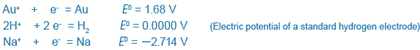
(An electron is expressed as “e” in Table 1, but “e^- ” is used here to clearly indicate that an electron is negatively charged.)

The values of E⁰ in these equilibrium relationships are values (standard oxidation-reduction potentials) calculated thermodynamically assuming that they are measured at standard conditions (at 25ºC and 1 atm) and the activity^* of each ion is 1.
However, this calculation requires a reference point, so these potential values are relative to the potential of a standard hydrogen electrode^** (S.H.E) or normal hydrogen electrode (N.H.E) or E⁰ (at 25ºC) set at 0.0000 V.
You can see that in these equilibrium systems gold (Au) has a tendency to exist as a metal (i.e., gold) and sodium (Na) as ions (i.e., sodium ions). One may think of gold jewelry and sodium ions present in seawater in large amounts (or salt, which is an ionic compound).
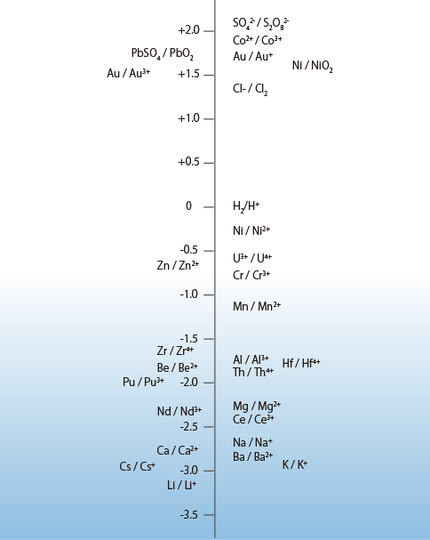
Figure 1 shows the oxidation-reduction potentials of substances in Table 1 arranged along a vertical axis. This figure allows you to understand the relative meanings of the oxidation-reduction potentials or that substances positioned higher on the vertical axis have a higher tendency to be reduced and substances positioned lower have a tendency to be oxidized.

* For details about activity, refer to “The Basis of pH - Definition of pH and Hydrogen-Ion Activity.”
** For details about standard hydrogen electrodes, refer to “The Basis of pH - Electrical Potential of Reference Electrode.”

Figure 1 Standard Oxidation-Reduction Potentials along a Vertical Axis (Excerpt from the cover sheet of a 1969 issue of “Electrochemistry”* (monthly magazine) (* This magazine is only available in Japanese. The title is a provisional translation.)

However, the ORP of an actual sample is decided by the equilibrium conditions of many different oxidants and reductants that coexist in the sample rather than a single equilibrium condition. Thus, ORPs cannot be explained in such a simple manner as above.

Next page  The Basis of ORP