
Equation of Cauchy Transparent
The earliest dispersion formula was established by Cauchy (1836) who set up simple empirical dispersion law. The “Cauchy Transparent” dispersion works best when the material has no optical absorption in the visible spectral range and consequently generally has a normal dispersion which means a monotonous decreasing refractive index with increasing wavelength in this way:
(1) 1 < n(λred)< n(λblue)
The following equation connects the refractive index to the wavelength (in nm):
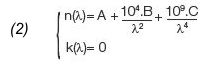
Equation of Cauchy Absorbent
A second formulation of the Cauchy model is the "Cauchy Absorbing" dispersion and it is more suitable to describe the optical properties of weakly absorbing materials. Here a non-zero extinction coefficient is given in an expression similar to the previous used for the refractive index:
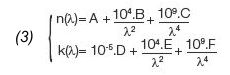
Three parameters are used in the equation of the Cauchy transparent model and 6 parameters in the Cauchy absorbing model.
Parameters describing the refractive index
(4) 0 < | C | < | B | < 1 < Α
Three parameters describe the extinction coefficient.
Cauchy’s formulation cannot be easily applied to metals and semiconductors. The parameters used do not have any physical meaning and therefore, these empirical relations are not Kramers-Kronig consistent. From first principles, the Kramers-Kronig relation relates the index of refraction and extinction coefficient parts; it means they are not independent quantities. In other words, if the value of the extinction coefficient is known over the entire spectral range, the index of refraction coefficient can be calculated.
Cauchy Transparent function
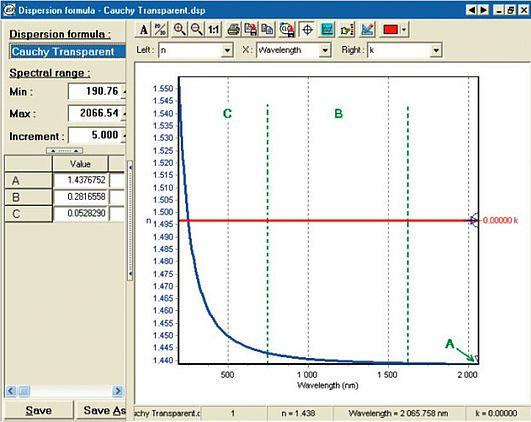
Fig. 15: Optical properties of SiO2given by the Cauchy transparent Function
Cauchy Absorbent function
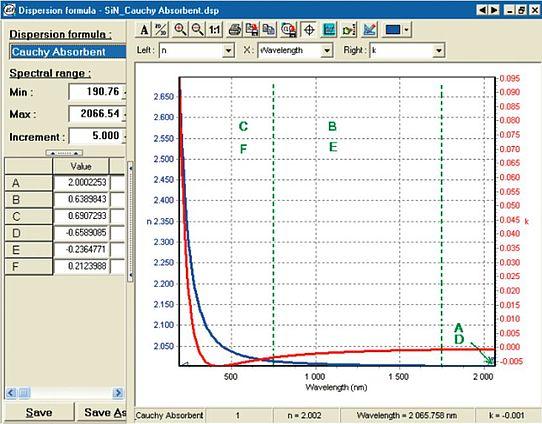
Fig. 16: Optical properties of SiN given by the Cauchy absorbent Function
The Cauchy model is used for transparent materials like insulators, glasses exhibiting no or very low optical absorption in the Far Ultra Violet.
References