Concentration of Hydrogen Ions

Next arises the question of what determines the acidity or alkalinity of a solution.
Actually, it is determined by the concentration of hydrogen ions, the percentage of hydrogen ions contained in the solution.
Let's take water as an example.
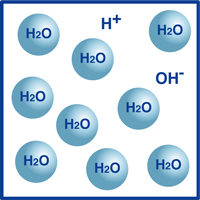
As you know, the formula for water is H2O. Most of the molecules in water are in that extremely stable form we know as H2O.
However, a very tiny percentage of those molecules have broken up into hydrogen ions (H+) and hydroxide ions, (OH-), as illustrated in the figure.
Actually, this balance of hydrogen ions and hydroxide ions determines the pH of the water.
When the hydrogen ions outnumber the hydroxide ions, the solution is acidic. If the reverse is true, then the solution is alkaline.
If the temperature does not vary, the following relationship between the densities of hydrogen ions (H+) and hydroxide ions (OH-) is found with any solution:
[H+][OH-]=Kw=10-14(=fixed) at 25℃
(Kw is called the ion product of water or dissociation constant of water.)
In pure water or neutral solution, the following formula holds true, because
[H+]=[OH-] ,
[H+]=[OH-]=√(Kw)=√10-14=10-7
If you know the value of either [H+] or [OH-], you can find the value of the other.
Thus, we measure only [H+] and use it as the standard for pH. In this way, pH is determined by hydrogen-ion concentration.

So, pH is defined by the following formula:
pH=-log10[H+]
The concentration of hydrogen ions in any solution we are likely to encounter will range from 1 mol to 0.000001 mol per liter of solution. However, solutions with extremely low hydrogen-ion concentration could conceivably rack up a pretty long parade of zeros after the decimal point. Danish biochemist S.P.L. Sorensen was the first to use the pH system we know today, which defines inverse numbers of hydrogen-ion concentration shown in common logarithm as pH. That is to say,
pH=-log10[H+]
In the case of a neutral solution,
[H+]=10-7 , which we call a pH of 7.
This means, for example, that a hydrogen-ion concentration of a solution with a pH of 4 is 10-4mol/l, meaning it contains 0.0001 mol of hydrogen ions in a solution of 1 liter. In the same way, a solution with a pH of 5 contains 10-5mol/l of hydrogen ions, a solution with a pH of 6 contains 10-6mol/l of hydrogen ions, while the solution with a pH of 7 contains 10-7mol/l of hydrogen ions. You will notice that if you compare solutions with pH of 4 and pH of 7, the difference in pH is only 3, but the concentration of hydrogen ions with a pH of 7 is 1000 times as high as with a pH of 4.The following figure also shows the advantage of exponents, which can express large variations in value that range over many orders of magnitude.
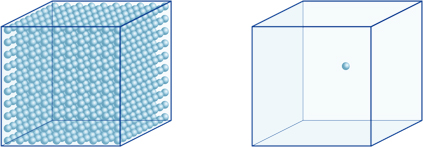
The number of hydrogen ions in the cube on the left (10-4mol/L) is 1,000 times larger than in the one on the right (10-7mol/L); this is equivalent to a difference of 3 in the pH value. (A single blue ball represents 10-7mol/L of hydrogen ions.)
Next page Hydrogen-Ion Activity