
Fig. 61a illustrates a tilted focal plane that may be present in Czerny-Turner monochromators.
For a monochromator system being used in spectrograph configuration with a solid state detector array, the user should be aware of the following:
Fig. 61a illustrates a tilted focal plane that may be present in Czerny-Turner monochromators. In the case of aberrationcorrected holographic gratings, γ, βH. and LH are provided as standard operating parameters.
Operating manuals for many Czerny-Turner (CZ) and Fastie-Ebert (FE) monochromators rarely provide information on the tilt of the focal plane, therefore, it may be necessary for the user to deduce the value of γ. This is most easily achieved by taking a well-known spectrum and iteratively substituting incremental values of ± γ, until the wavelength appearing at each pixel corresponds to calculated values.
The terms used below are consistent for aberration-corrected holographic concave gratings as well as Czerny-Turner and Fastie-Ebert spectrometers.
λC - Wavelength (in nm) at center of array (where exit slit would usually be located)
LA - Entrance arm length (mm)
LBλn - Exit arm length to each wavelength located on the focal plane (mm)
LBλc - Exit arm length to λc (CZ and FE monochromators LA = LBλc = F)
LH - Perpendicular distance from grating or focusing mirror to the focal plane (mm)
F - Instrument focal length. For CZ and FE monochromators LA = F = LB. (mm)
βH - LH - Angle from LH to the normal to the grating (this will vary in a scanning instrument)
βλn - Angle of diffraction at wavelength n
βλc - Angle of diffraction at center wavelength
HBλn - Distance from the intercept of the normal to the focal plane to the wavelength λn
HBλc - Distance from the intercept of the normal to the focal plane to the wavelength λc
Pmin - Pixel # at extremity corresponding to λmin (e.g., # 1)
Pmax - Pixel # at extremity corresponding to λmax (e.g., # 1024)
Pw - Pixel width (mm)
Pc - Pixel # at λc (e.g., # 512)
Pλ - Pixel # at λn
γ - Inclination of the focal plane measured at the location normally occupied by the exit slit, λc. (This is usually the center of the array. However, provided that the pixel marking this location is known, the array may be placed as the user finds most useful).
For this reason, it is very convenient to use a spectrometer that permits simple interchange from scanning to spectrograph by means of a swing away mirror. The instrument may then be set up with a standard slit using, for example, a mercury lamp. Switching to spectrograph mode enables identification of the pixel, Pc, illuminated by the wavelength previously at the exit slit.
The equations that follow are for Czerny-Turner type instruments where γ = 0° in one case and γ ≠ 0° in the other.
Case 1 γ = 0°
See Fig. 61b.
LH = LB = F at λc (mm)
βH = β at λc
HBλn = Pw (Pλ - Pc) (mm)
HB is negative for wavelengths shorter than λc.
HB is positive for wavelengths longer than λc.
(70) βλn = βH - tan-1(HBλn/LH)
Note: The secret of success (and reason for failure) is frequently the level of understanding of the sign convention. Be consistent and make reasonably accurate sketches whenever possible.
To make a calculation, α and β at λc can be determined from Equations (2), (19). At this point, the value for α is used in the calculation of all values βλn for each wavelength.
Then,
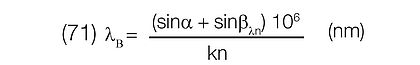
Case 2: γ does not equal 0°
See Fig. 61a).
LH = cosγ (where F = LBλc)
βH = βλc + γ
HBλc = Fsinγ
HBλn = Pw(Pλ - Pc) + HBλc
λn = βH - tan-1(HBλn / LH)
Again, keeping significant concern for the sign of HBλn, proceed to calculate the value Bλn after first obtaining α at λc then use Equation (71) to calculate λn.
IN PRACTICE, THIRD AND FOURTH DECIMAL PLACE ACCURACY IS NECESSARY.
Indeed the longer the instrument’s focal length, the greater the contribution of rounding errors.
To illustrate the above discussion a worked example, taken from a readily available commercial instrument, is provided.
Example:
The following are typical results for a focal plane inclined by 2.4° in a Czerny-Turner monochromator used in spectrograph mode.
LB = 320 mm at λc = F
n = 1800 g/mm
D = 24°
LH = 319.719 mm
γ = 2.4°
HBλc = 13.4 mm
Array length = 25.4 mm; λc appears 12.7 mm from end of array
λmin, λmax = wavelength at array extremities
λerror min, max = wavelength thought to be at array extremity if γ = 0°
Disp = dispersion (Equation (5)) (nm/mm)
mag = magnification in dispersion plane (Equation (32))
Δλ(γ = 0°) = λmin or λmax - λerror (nm)
Δd = Actual distance of λerror from extreme pixel (μm)
Operating Parameters for a CZ Spectrometer with a 2.4° Tilt at λc on the Spectral Plane Compared to a 0° Tilt.
Examination of the results given in the worked example indicates the following phenomena:
If an array with 25 μm pixels was used and the focal plane was assumed to be normal to λc rather than the actual 2.4°, at least a one pixel error (32 μm) would be present at λmin (this may not seem like much, but it is incredible how much lost sleep and discussion time has been spent attempting to rationalize this dilemma).
A 25 μm entrance slit is imaged in the focal plane with a width of 27.25 μm (1.09 × 25) at 229.946 nm (when λc = 250 nm) but is imaged with a width of 37.75 μm at 713.2nm (1.51 × 25) (when λc = 700 nm), Indeed in this last case the difference in image width at λmin compared to λmax varies by over 10% across the array.
If the array did not limit the resolution, then a 25 μm entrance slit width would produce a bandpass of 0.04 nm. Given that, in the above example with γ = 0° rather than 2.4°, the wavelength error at λmin exceeds 0.04 nm. Therefore, a spectral line at this extreme end of the spectral field could “disappear” the closer λc comes to the location of the exit slit.
The spectral coverage over the 25.4 mm array varies in the examples and are calculated as follows:
| λc (nm) | (λmax - λmin) (nm) |
| 250 | 39.80 |
| 400 | 36.67 |
| 700 | 27.04 |
In this case, provided λc is known, α, βH, and LH may be determined as above. If λn is known, the βλn may be obtained from the Grating Equation, Equation (1). Then
(72) HBλn =LH tan (βH - βλn)
This formula is most useful for constructing alignment targets with the location of known spectral lines marked on a screen or etched into a ribbon, etc.
Você tem alguma dúvida ou solicitação? Utilize este formulário para entrar em contato com nossos especialistas.