
If a light source emits a spectrum which consists of a single monochromatic wavelength λo (Fig. 23) and is analyzed by a perfect spectrometer, the output should be identical to the spectrum of the emission (Fig. 24) which is a perfect line at precisely λo.
In the most fundamental sense both bandpass and resolution are used as characterization of an instrument's ability to separate adjacent spectral lines.
Assuming a continuum light source, the bandpass (BP) of an instrument is the spectral interval that may be isolated. This depends on many factors including the width of the grating, system aberrations, spatial resolution of the detector, and entrance and exit slit widths.
If a light source emits a spectrum which consists of a single monochromatic wavelength λo (Fig. 23) and is analyzed by a perfect spectrometer, the output should be identical to the spectrum of the emission (Fig. 24) which is a perfect line at precisely λo.
In reality, spectrometers are not perfect and produce an apparent spectral broadening of the purely monochromatic wavelength. The line profile now has finite width and is known as the “instrumental line profile” (instrumental bandpass) (Fig.26).
The instrumental profile may be determined in a fixed grating spectrograph configuration with the use of a reasonably monochromatic light source such as a single mode dye laser. For a given set of entrance and exit slit parameters, the grating is fixed at the proper orientation for the central wavelength of interest and the laser light source is scanned in wavelength. The output of the detector is recorded and displayed. The resultant trace will show intensity versus wavelength distribution.
For a monochromator, the same result would be achieved if a monochromatic light source is introduced into the system and the grating rotated.
The bandpass is then defined as the Full Width at Half Maximum (FWHM) of the trace, assuming monochromatic light.
Any spectral structure may be considered to be the sum of an infinity of single monochromatic lines at different wavelengths. Thus, there is a relationship between the instrumental line profile, the real spectrum and the recorded spectrum.
Let B(λ) be the real spectrum of the source to be analyzed.
Let F(λ) be the recorded spectrum through the spectrometer.
Let P(λ) be the instrumental line profile.
(34) F = B * P
The recorded function F(λ) is the convolution of the real spectrum and the instrumental line profile.
The shape of the instrumental line profile is a function of various parameters:
Each of these factors may be characterized by a special function Pi(λ), each obtained by neglecting the other parameters. The overall instrumental line profile P(λ) is related to the convolution of the individual terms:
(35) P(λ) = P1(λ).P2(λ)...Pn(λ)
Spectrometers produce an apparent spectral broadening of the purely monochromatic wavelength. The line profile now has finite width and is known as the "instrumental line profile" (instrumental bandpass).
Selection of the wavelength in function of the exit slit.
If the slits are of finite width and there are no other contributing effects to broaden the line, and if:
Went = width of the image of the entrance slit
Wex = width of the exit slit or of one pixel in the case of a
multichannel detector
Δλ1 = linear dispersion × Went
Δλ2 = linear dispersion × Wex
then the slit's contribution to the instrumental line profile is the convolution of the two slit functions (see Fig. 26).
If the two slits are infinitely narrow and aberrations negligible, then the instrumental line profile is that of a classic diffraction pattern. In this case, the resolution of the system is the wavelength, λ, divided by the theoretical resolving power of the grating, R (11).
If the two slits are infinitely narrow and broadening of the line due to aberrations is large compared to the size due to diffraction, then the instrumental line profile due to diffraction is enlarged.
In practice, the FWHM of F(λ) is determined by the convolution of the various causes of line broadening including:
dλ (resolution): the limiting resolution of the spectrometer is governed by the limiting instrumental line profile and includes system aberrations and diffraction effects.
dλ (slits): bandpass determined by finite spectrometer slit widths.
dλ (line): natural line width of the spectral line used to measure the FWHM.
Assuming a Gaussian line profile (which is not the case), a reasonable approximation of the FWHM is provided by the relationship:
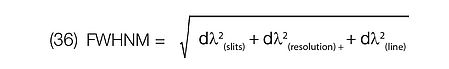
In general, most spectrometers are not routinely used at the limit of their resolution so the influence of the slits may dominate the line profile. From Figure 18, the FWHM, due to the slits, is determined by either the image of the entrance slit or the exit slit, whichever is greater. If the two slits are perfectly matched and aberrations minimal compared to the effect of the slits, then the FWHM will be half the width at the base of the peak. (Aberrations may, however, still produce broadening of the base). Bandpass (BP) is then given by:
BP = FWHM ~ linear dispersion × (exit slit width or the image of the entrance slit, whichever is greater).
Prevouisly, image enlargement through the spectrometer was reviewed. The impact on the determination of the system bandpass may be determined by taking Equation (32) to calculate the width of the image of the entrance slit and multiplying it by the dispersion (Fig. 5).
Bandpass is then given by:
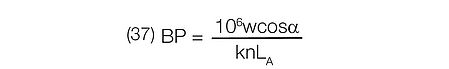
The major benefit of optimizing the exit slit width is to obtain maximum THROUGHPUT without loss of bandpass. It is interesting to note from Equations (37) and (5) that:
• Bandpass varies as cos α
• Dispersion varies as cos β
Expected Spectral Coverage & Resolution with a Synapse or Symphony CCD.
Because the image in the exit plane changes in width as a function of wavelength, the user of an array type detector must be aware of the number of pixels per bandpass that are illuminated. It is normal to allocate 3-6 pixels to determine one bandpass. If the image increases in size by a factor of 1.5, then photons contained within that bandpass would have to be collected over 4-9 pixels. The FWHM that determines bandpass is equivalent to the width of the image of the entrance slit containing a typical maximum of 80% of available photons at the wavelength of interest; the remainder is spread out in the base of the peak. Any image magnification, therefore, equally enlarges the base, spreading the entire peak over additional pixels.
The infinitely narrow natural spectral band width of monochromatic light is, by definition, less than that of the instrumental bandpass determined by Equation (36). (A very narrow band width is typically referred to as a “line” because of its appearance in a spectrum).
In this case all the photons present will be at exactly the same wavelength irrespective of how they are spread out in the exit plane. The image of the entrance slit, therefore, will consist exclusively of photons at the same wavelength even though there is a finite FWHM. Consequently, bandpass in this instance cannot be considered as a wavelength spread around the center wavelength. If, for example, monochromatic light at 250 nm is present and the instrumental bandpass is set to produce a FWHM of 5 nm, this does NOT mean 250 nm ± 2.5 nm because no wavelength other than 250 nm is present. It does mean, however, that a spectrum traced out (wavelength vs. intensity) will produce a “peak” with an apparent FWHM of “5 nm” due to instrumental and NOT spectral line broadening.
Emission lines with finite natural spectral bandwidths are routinely found in almost all forms of spectroscopy including emission, Raman, fluorescence, and absorption.
In these cases, spectra may be obtained that seem to consist of line emission (or absorption) bands. If, however, one of these “lines” is analyzed with a very high-resolution spectrometer, it would be determined that beyond a certain bandpass no further line narrowing would take place indicating that the natural bandwidth had been reached.
Depending on the instrument system, the natural bandwidth may or may not be greater than the bandpass determined by Equation (36).
If the natural bandwidth is greater than the instrumental bandpass, then the instrument will perform as if the emission “line” is a portion of a continuum. In this case the bandpass may indeed be viewed as a spectral spread of ± 0.5 BP around a center wavelength at FWHM.
Strip chart recording plotting wavelength versus intensity where BP = FWHM (in mm) x Dispersion.
The following figure shows a somewhat contrived spectrum where the first two peaks are separated on the recording by 32 mm. The FWHM of the first peak is the same as the second but is less than the third. This implies that the natural bandwidth of the third peak is greater than the bandpass of the spectrometer and would not demonstrate spectral narrowing of its bandwidth even if evaluated with a very high resolution spectrometer.
The first and second peaks, however, may well possess natural bandwidths less than that shown by the spectrometer. In these two cases, the same instrument operating under higher bandpass conditions (narrower slits) may well reveal either additional “lines” that had previously been incorporated into just one band, or a simple narrowing of the bandwidth until either the limit of the spectrometer or the limiting natural bandpass have been reached.
Variation of Dispersion and Slit Width to Produce 0.16 nm Bandpass in a 320 mm Focal Length Czerny-Turner.
A researcher finds a spectrum in a journal that would be appropriate to reproduce on an in-house spectrometer. The first task is to determine the bandpass displayed by the spectrum. If this information is not given, then it is necessary to study the spectrum itself.
Assuming that the wavelengths of the two peaks are known, then the distance between them must be measured with a ruler as accurately as possible. If the wavelength difference is found to be 1.25 nm and this increment is spread over 32 mm (Fig. 28), the recorded dispersion of the spectrum = 1.25/32 = 0.04 nm/mm. It is now possible to determine the bandpass by measuring the distance in mm at the Full Width at Half Maximum height (FWHM). Let us say that this is 4 mm; the bandpass of the instrument is then 4 mm x 0.04 nm/mm = 0.16 nm.
Also assuming that the spectrometer described in Table 4 is to be used, then from Equation (37) and the list of maximum wavelengths described in Table 6, the following options are available to produce a bandpass of 0.16 nm:
The best choice would be the 3600 g/mm option to provide the largest slit width possible to permit the greatest amount of light to enter the system.
Você tem alguma dúvida ou solicitação? Utilize este formulário para entrar em contato com nossos especialistas.