

Dynamic light scattering (DLS) results are often expressed in terms of the Z-average. The Z-average arises when DLS data is analyzed by the use of the technique of cumulants (1). Since the calculation of the Z-average is mathematically stable, the Z-average result is insensitive to noise, and that makes it a preferred DLS size parameter. The purpose of this document is to clarify the meaning of this value.
Do you need to determine Z-average size? Take a look at the nanoPartica SZ-100V2 for a description of a world class tool.
The Z-average can be expressed as the intensity based harmonic mean (2,3) and is shown by the equation below:
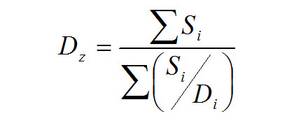
Here, Si is the scattered intensity from particle i and Di is the diameter of particle i. Note that the result is in the form of a harmonic mean. Since this mean is calculated from the intensity weighted distribution, leading to the statement that the Z-average size is the intensity weighted harmonic mean size. For the case of sufficiently small particles known as Rayleigh scatterers, Si ~ Di6. Therefore, the Z-average can be approximated as:
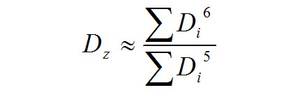
There are two points about the use of the term “Z-average.” The first is that the use of the term Z-average in DLS does not match the use of the term when one is using light scattering to analyze polymers. The second is that one occasionally finds other notation, such as xDLS or dDLS. Even so, “Z-average” is the most common term.
In Figure 2 we illustrate the Z-average with a calculation showing a lognormal size distribution. A volume weighted differential size distribution is shown in blue. A discussion of different distribution types can be found in HORIBA TN154.
The example distribution’s median (Dv,50) size is indicated as 100 nm. From this distribution, we calculate the scattered intensity for each particle size (4). This intensity based distribution is then plotted in green. Finally, the harmonic mean of the intensity-based distribution is indicated at 97 nm. Note that the Z-average size is close to, but does not equal Dv,50.
The Z-average size value is calculated by the methods of cumulants (1). Since this technique relies on numerically stable least squares fitting, it is relatively insensitive to experimental noise.
In cumulants analysis the baseline subtracted autocorrelation function, C, is treated as an exponential decay of the following form:

Here, C is the baseline subtracted autocorrelation function and τ is delay time. Values for A, Γ, and µ2 can be readily obtained by a least squares fit. One then finds the intensity weighted average diffusion coefficient Dt,avg. with the relation Γ=Dt,avg. q2. Here q is the scattering vector given by q= (4πn/λ)sin(θ/2). The refractive index of the liquid is n. The wavelength of the laser light is λ, and scattering angle, θ. Finally, one uses the Stokes-Einstein relation to go from Dt to Z-average particle size, Dz.
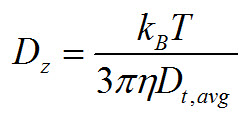
where
Unfortunately, the weighting of the average is somewhat convoluted. Recall that the decay constant is proportional to the diffusion coefficient. So, by DLS one has determined the intensity weighted diffusion coefficient. The diffusion coefficient is inversely proportional to size. Therefore, the “Z-average size” is the intensity weighted harmonic mean size.
Despite the convoluted meaning, the Z-average size increases as the particle size increases. Therefore it provides a reliable measure of the average size of a particle size distribution. Also, it is easily measured. For these reasons, the Z-average size has become the accepted norm for presenting particle sizing results by DLS.
The HORIBA SZ-100V2 Nanoparticle Analyzer also presents size measurement results as a distribution table and graph and calculated mean diameter or diameters for multi-modal distributions. The methods behind those calculations are beyond the scope of this work.
(1) Koppel, D.E. “Analysis of Macromolecular Polydispersity in Intensity Correlation Spectroscopy: The Method of Cumulants” J. Chem. Phys 57 (11), pp 4814-4820, 1972.
(2) ISO 22412:2008 Particle Size Analysis – Dynamic Light Scattering
(3) Thomas, J. C. “The determination of log normal particle size distributions by dynamic light scattering” J. Colloid Interface Sci. 117 (1) pp 187-192 (1987)
(4) Here the Rayleigh-Debye-Gans approach is used and a larger average particle size is chosen to illustrate the regime where the approximations in equation 2 do not apply. This calculation is for particles in water, a 532 nm laser, and a 90 degree scattering angle.
Nanoparticle Analyzer
Do you have any questions or requests? Use this form to contact our specialists.
