
To understand how a complete monochromator system is characterized, it is necessary to start at the transfer optics that brings light from the source to illuminate the entrance slit (see Fig. 20). Here we have “unrolled” the system and drawn it in a linear fashion.
Typical Monochromator System.
AS - aperture stop
L1 - lens 1
M1 - mirror 1
M2 - mirror 2
G1 - grating
p - object distance to lens L1
q - image distance from lens L1
F - focal length of lens L1 (focus of an object at infinity)
d - the clear aperture of the lens (L1 in diagram)
Ω - half-angle
s - area of the source
s’ - area of the image of the source
An aperture stop (AS) limits the opening through which a cone of light may pass and is usually located adjacent to an active optic. A pupil is either an aperture stop or the image of an aperture stop.
The entrance pupil of the entrance (transfer) optics in Fig. 20 is the virtual image of An aperture stop (AS) as seen axially through lens L1 from the source.
The entrance pupil of the spectrometer is the image of the grating (G1) seen axially through mirror M1 from the entrance slit.
The exit pupil of the entrance optics is An aperture stop (AS) itself seen axially from the entrance slit of the spectrometer. The exit pupil of the spectrometer is the image of the grating seen axially through M2 from the exit slit.
Relationship between f/value, half-angle, and numerical aperture.
The light gathering power of an optic is rigorously characterized by Numerical Aperture (NA). Numerical Aperture is expressed by:
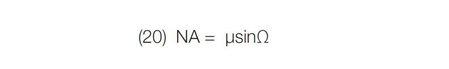
where μ is the refractive index (μ =1 in air)
and f/value by:
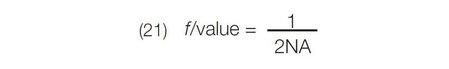
f/value is also given by the ratio of either the image or object distance to the diameter of the pupil. When, for example, a lens is working with finite conjugates such as in Fig. 20, there is an effective f/value from the source to L1 (with diameter AS) given by:

And the effective f/value from L1 to the entrance slot is given by:

In the sections that follow, f/value will always be calculated assuming that the entrance or exit pupils are equivalent to the aperture stop for the lens or grating, and the distances are measured to the center of the lens or grating.
When the f/value is calculated in this way for f/2 or greater (e.g. f/3, f/4, etc.), then sin Ω is ~ tan Ω and the approximation is good. However, if an active optic is to function at an f/value significantly less than f/2, then the f/value should be determined by first calculating Numerical Aperture from the half-angle.
The widths W' and W'' are the projections of the grating width as perceived at the entrance and exit slits, respectively.
Because the angle of incidence alpha is always different in either sign or value from the angle of diffraction beta (except in Littrow), the projected size of the grating varies with the wavelength and is different depending on whether it is viewed from the entrance or exit slits.
In Fig. 21, the widths W' and W'' are the projections of the grating width as perceived at the entrance and exit slits, respectively.
To determine the f/value of a spectrometer with a rectangular grating, it is first necessary to calculate the “equivalent diameter,” D', as seen from the entrance slit and D" as seen from the exit slit. This is achieved by equating the projected area of the grating to that of a circular disc and then calculating the diameter D' or D".
(24) Wg’= Wg cosα = Projected area of grating from entrance slit
(25) Wg” = Wg cosβ = Projected area of grating from exit slit
In a spectrometer, therefore, the f /valuein will not equal the f /valueout.
(26) f /valuein = LA/D’
(27) f /valueout = LB/D”
where, for a rectangular grating, D' and D" are given by:
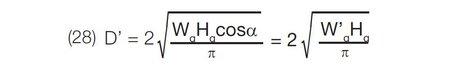
where, for a circular grating, D' and D" are given by:
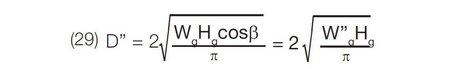
Calculated values for f/valuein and f/valueout for a Czerny-Turner configuration with 68 x 68 mm, 1800 g/mm grating and LA = LB = F = 320 nm. Dv = 24°.
Table 3 shows how the f/value changes with wavelength.
In any spectrometer system, a light source should be imaged onto an entrance slit (aperture) which is then imaged onto the exit slit and so on, to the detector, sample, etc. This process inevitably results in the magnification or demagnification of one or more of the images of the light source. Magnification may be determined by the following expansions, taking as an example the source imaged by lens L1 in Fig. 20 onto the entrance slit:
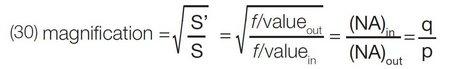
Similarly, flux density is determined by the area that the photons in an image occupy, so changes in magnification are important if a flux density sensitive detector or sample are present. Changes in the flux density in an image may be characterized by the ratio of the area of the object, S, to the area of the image, S', from which the following expressions may be derived:
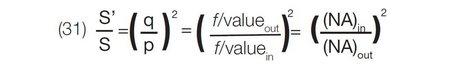
These relationships show that the area occupied by an image is determined by the ratio of the square of the f/values. Consequently, it is the exit /value that determines the flux density in the image of an object. Those using photographic film as a detector will recognize these relationships in determining the exposure time necessary to obtain a certain signal-to-noise ratio.
Anamorphic optics magnify (or demagnify) a source by different factors in the vertical and horizontal planes.
Anamorphic optics are those optics that magnify (or demagnify) a source by different factors in the vertical and horizontal planes (see Fig. 22).
In the case of a diffraction grating-based instrument, the image of the entrance slit is NOT imaged 1:1 in the exit plane (except in Littrow and perpendicular to the dispersion plane assuming LA = LB).
This means that in virtually all commercial instruments, the tradition of maintaining equal entrance and exit slit widths may not always be appropriate.
Geometric horizontal magnification depends on the ratio of the cosines of the angle of incidence, alpha, and the angle of diffraction, beta, and the LB/LA ratio (Equation (32)). Magnification may change substantially with wavelength (see Table 4).
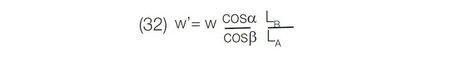
Relationship Between Dispersion, Horizontal Magnification, and Bandpass in a Czerny -Turner Monochromator.
Table 4 illustrates the relationship between alpha, beta, dispersion, horizontal magnification of entrance slit image, and bandpass.
Exit slit width matched to image of entrance slit.
* As the inclination of the grating becomes increasingly large, coma in the system will increase. Consequently, in spite of the fact that the bandpass at 800 nm is superior to that at 200 nm, it is unlikely that the full improvement will be seen by the user in systems of less than f/8.
Slit height magnification is directly proportional to the ratio of the entrance and exit arm lengths and remains constant with wavelength (exclusive of the effects of aberrations that may be present).
(33) h’ = (LB / LA)h
Note: Geometric magnification is not an aberration!
HORIBA제품의 자세한 정보를 원하시면, 아래의 양식에 내용을 입력을 부탁드립니다.