
柯西透明方程
The earliest dispersion formula was established by 最早的色散公式是有柯西1836年建立的,他建立了简单的经验色散定律。当材料在可见光范围内没有吸收时,“柯西透明”色散的效果最好,通常具有标准的色散,这意味折射率随着波长的增加而降低。如下方公式:
(1) 1 < n(λ红)< n(λ蓝)
折射率与波长(nm)的关系遵循下方方程:
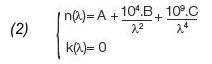
柯西吸收方程
柯西模型的第二个公式是 “柯西吸收”色散,它更适合描述弱吸收材料的光学特性。这里消光系数非零,其表达式与上述的折射率方程类似:
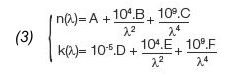
柯西透明模型方程中使用了3个参数,柯西吸收模型方程中使用了6个参数
描述折射率的三个参数
(4) 0 < | C | < | B | < 1 < Α
描述消光系数的三个参数
柯西的公式并不适用于金属和半导体材料,使用的参数没有任何物理意义,并且这些经验关系与Kramers-Kronig不一致。从第一性原理出发,Kramers-Kronig关系将折射率和消光系数关联起来,这就说明它们不是独立的量。换言之,已知整个光谱范围的消光系数值就可以计算出折射率。
柯西透明函数

图15:柯西透明函数获得的SiO2光学特性
柯西吸收函数

图16:柯西吸收函数获得的SiN光学特性
柯西模型通常用于透明材料,如绝缘体、玻璃在远紫外没有或吸收很低的材料。
参考文献